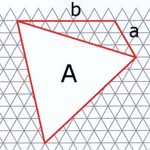
Figure 52
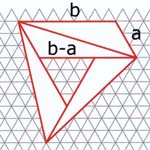
Figure 53
So, how about scaling in 3-fold rotational systems, like the Chinese men and the lizards: can we make six lizards out of three Chinese men? First, remember that we need some kind of nice, regular connection between the symmetry points in both layers. The combination of two different scaled hexagonal lattices in Figure 52 a,b,c seems to give a solution, but exact calculation shows that the areas of the big grey hexagons and the black hexagons are in the proportion of 4 to 7.

In general, using an isometric grid of equilateral triangles and following the reasoning for the square grids, since any equilateral triangle can be divided into axa + bxb + ab small equilateral triangles (see Figures 53), we can only use combinations of numbers from the series (of areas) 1, 3, 4, 7, 9, 12, 13, 16, 19, that are shown in Table 2.
a \ b
0
1
2
3
4
0
0
1
4
9
16
1
1
3
7
13
21
2
4
7
12
19
20
3
9
13
19
27
37
4
16
21
20
37
48
5
25
        
Table 2. The table entries are axa + bxb + ab
And so there is no way to just double the number of lizards.
Figure 52a
Figure 52b
Figure 52c