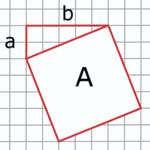
Figure 51
To answer this, draw a big square on a square grid, so that the corner points of the big square are on grid points, as shown in Figure 51. Now measure the area of the big square in small square units. By the Pythagorean Theorem, this area is axa + bxb. This means that we can divide any such big square into axa + bxb small squares where a and b are non-negative integers. And this leads to the series of areas of large squares: 1, 2, 4, 5, 8, 9, 10, as you can read from Table 1.
|
a \ b
|
0
|
1
|
2
|
3
|
4
|
|
0
|
0
|
1
|
4
|
9
|
16
|
|
1
|
1
|
2
|
5
|
10
|
17
|
|
2
|
4
|
5
|
8
|
13
|
20
|
|
3
|
9
|
10
|
13
|
18
|
25
|
|
4
|
16
|
17
|
20
|
25
|
32
|
|
5
|
25
|
Table 1. The table entries are axa + bxb
In our example of turning four fish into eight birds, we began by making a square grid on each tessellation by joining the rows of centers of 2-fold and four-fold rotations (see Figures 38 and 43). Note that each square in these grids has area equal to exactly one motif (one bird or one fish), so each square can represent one motif. Consider the square grid of fish as the small squares in Figure 51 and then enlarge the scale of the bird tessellation so that a cluster of four birds (four bird-squares) centered at a 4-fold rotation point fits the large square shown in Figure 51, with a = b = 2. Then the large square contains four birds and 2x2 + 2x2 = 8 fish. Also notice that 4-fold centers of the two tessellations are superimposed.
Four birds can be changed into eight fish because the large square built on the hypotenuse of the 2x2 right triangle has the property that 4-fold centers of the large grid are superimposed on those of the small grid. Any pair of numbers m, n chosen from Table 1 which allow this kind of superpositon may be used for tessellations with 4-fold rotations to turn m motifs into n motifs.