4. New Polyhedra

4.1. Strips of Equilateral Triangles. To construct the helical deltahedra we can start with any number of side-by-side connected strips of equilateral triangles. In Figures 12-14 we show the process of folding a helical deltahedron with five strips. When we can connect the left edge of the left-most strip to the right edge of the right-most strip in such a way that the triangles become connected edge to edge, the final helical deltahedra is formed.
Figure 12: Five Strips
Figure 13: Folding
Figure 14: Helical Deltahedron
After we have reached the situation in Figure 14, we can continue to make the folding edges sharper. The strips will now intersect as can be seen in Figure 15-16, and at a certain moment the original left-most edge can be connected to the original right-most edge again (Figure 17). The final new polyhedron is a uniform polyhedron. All faces are equal and the vertices are all congruent.
Figure 15: Intersecting
Figure 16: Almost closed
Figure 17: Helical Star Deltahedron
4.2. Shift. Depending on the number of strips you begin with, there is usually more than one way to connect the left-most edge of the set of strips to the right-most edge. There has to be a shift to get a helical deltahedron. But the number of steps in this shift may vary (Figure 18-20). Starting with five strips there are two possibilities to create a helical deltahedron in which faces do not intersect with other faces.
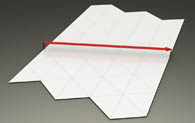
Figure 18: 5 Strips of Triangles
Figure 19: Connection a
Figure 20: Connection b
Also for the new structure, with the intersection, there are two ways to create a regular polyhedron. They are shown in Figure 21 and 22. Because of the star shape in the polyhedron I will call this new family of regular polyhedra “helical star deltahedra”.
Figure 21: Helical Star Deltahedron 5-2(1)
Figure 22: Helical Star Deltahedron 5-2(2)
4.3. Stars. Figure 23 shows an overview of regular star polygons is shown starting from 5-2 up to 12-5.