Figure 62
Figure 63a
Figure 63b
Figure 64
Figure 65
Figure 66
Figure 67
Figure 68a
Figure 68b
|
|
|
|
|
|
|
|||||||||
|
|||||||||||||||
|
|
|
|
||||||||||||
|
|
||||||||||||||
|
Figure 62
|
Figure 63a
|
Figure 63b
|
|||||||||||||
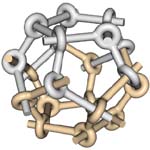
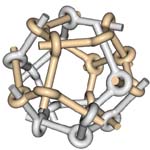
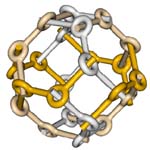
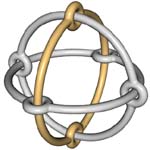
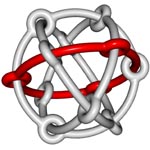
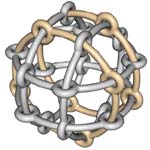
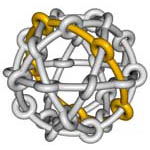
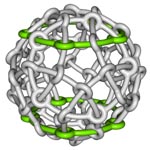
| With finite bar grid systems (in which the bars are necessarily bent so that they can be connected according to the rules), we can construct some of the regular and semi-regular polyhedra, a favorite subject of both M. C. Escher and Leonardo da Vinci. Polyhedra in which three faces meet at each vertex can be constructed with da Vinci's noncrossing-type bar grid: Figure 62 shows a tetrahedron, Figure 63 a,b a dodecahedron, and Figure 64 a truncated octahedron. Polyhedra in which four faces meet at each vertex can be constructed with Escher's crossing-type bar grids. In the figures that show some examples, a single closed loop of one bar is highlighted. Figure 65 shows an octahedron, Figure 66 a cuboctahedron, Figure 67 a rhombicuboctahedron, and Figure 68 a truncated dodecahedron. | |||||||||||||||
|
|
|
|||||||||||||
|
Figure 64
|
Figure 65
|
Figure 66
|
|||||||||||||
|
|
|
|||||||||||||
|
Figure 67
|
Figure 68a
|
Figure 68b
|
|||||||||||||
|
|||||||||||||||