


Figure 22
Figure 23
Figure 24
Interwoven tiling-lattices can be constructed in several ways. The number of layers is one thing we can vary. The tiling-lattice with the large and small square holes (Figure 2) can be interwoven with different numbers of copies: while Figure 5 has two layers interwoven, Figure 22 has four. Figures 23 and 24 are constructed from the planar tiling-lattice that is the basis for Figure 16, but there are three layers in Figure 23 and seven in Figure 24.



Figure 25
Figure 26
Figure 27
Another technique, of which we will see more examples later on, is to use copies of the same tiling-lattice, with some at a different scale. In Figure 25, there are four congruent layers of the tiling-lattice for the familiar Archimedean tiling by squares and octagons. In Figure 26, three layers of the same tiling-lattice are used, but the grey layer is at a smaller scale.
The most interesting interwoven tiling-lattices are made by combining more than one type of tiling-lattice. For example, Figure 27 is a combination of the right-turning version and the left-turning version of the same lattice (see Figure 2). In Figure 28, the tiling-lattice in Figure 2 is combined with the octagon-square tiling-lattice, In Figures 29 and Figure 30 you can see the black and white hexagonal tiling-lattices of Escher (Figure 6) combined with lattices with square and octagonal holes.

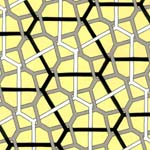

Figure 28
Figure 29
Figure 30



Figure 30a
Figure 30b
Figure 30c