Elevations and Stellations

Abstract

Stellation is a well known operation which you can apply to a polyhedron. About a century before this operation was defined by Kepler, Luca Pacioli and Leonardo da Vinci had published the book “La Divina Proportione” in which another operation, called Elevation, was described. Both operations have much in common, but there are also many differences. Comparing both operations inspired me to define a new one, which I called Edge Elevation. This led to interesting artistic constructions.

1. Introduction

1.1. Elevation. In their book “La Divina Proportione” [1] Luca Pacioli and Leonardo da Vinci introduced the elevated versions of all of the Platonic polyhedra as well as of some of the Archimedean polyhedra. The Platonic solids as well as their elevations as they are drawn by Leonardo da Vinci are shown in Figure 1a and 1b.
Figure 1a: The Platonic Solids
Figure 1b: Elevations of the Platonic Solids
What exactly is an elevated version of a polyhedron? In “La Divina Proportione” [2],chapter XLIX, paragraph XI.XII, Pacioli describes the elevated version of the cube as follows: “… it is enclosed by 24 triangular faces. This polyhedron is built out of 6 four-sided pyramids, together building the outside of the object as you can see it with your eyes. And there is also a cube inside, on which the pyramids are placed. But this cube can only be seen by imagination, because it is covered by the pyramids. The 6 square faces are the bottom faces of the 6 pyramids.”. So in total this object is composed of 24 equilateral triangular faces plus 6 hidden square faces, as can be seen in the exploded views in Figure 2.
Figure 2: Exploded views of the elevated cube.
Figure 3: Exploded views of the elevated octahedron.
About the “Octocedron Elevatus”, Pacioli writes (Chapter L, paragraph XIX.XX): “And this object is built with 8 three-sided pyramids, that can be seen with your eyes, and an octahedron inside, which you can only see by imagination.”. This means that the object is composed of 32 equilateral triangular faces of which 8 are hidden.
1.2. Stellation. Pacioli doesn’t give a real definition of “Elevation” but his descriptions are very clear.
In 1619, about one century later, Kepler defined “Stellation” for polygons and polyhedra as the process of extending edges or faces until they meet to form a new polygon or polyhedron [3]. Following the definition of Kepler, the stellation of the octahedron has the same number of faces as the octahedron itself since the eight triangular faces are extended to eight bigger triangular faces. These large triangular faces intersect each other, forming the so-called Stella Octangula or Kepler Star. As we can also see in M.C. Escher’s print "Two Worlds", this object is in fact a combination of two interpenetrating tetrahedra.
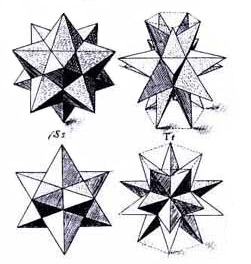
Figure 4: Kepler's Stellations
Figure 5: M.C. Escher's Gravity Star