3. Archimedean Tiling Patterns

3.1. Weaving Structures. The concept of elevation applied to flat patterns leads to interesting weaving. Elevation of squares, like in Da Vinci’s elevated cube, leads to the pattern of Figure 18. But in the plane there are many tiling patterns that can be studied now.
Figure 17: More regular tiling patterns.
Figure 18: Square pattern.
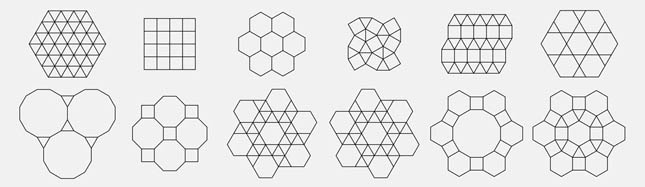
We will start examining the possibilities of elevation of the Archimedean patterns and the duals of these patterns (Figure 19). As in the elevations of Luca Pacioli and Leonardo da Vinci, I will limit myself to tiles with 3, 4 or 5 edges.
Figure 19: Archimedean tiling patterns.
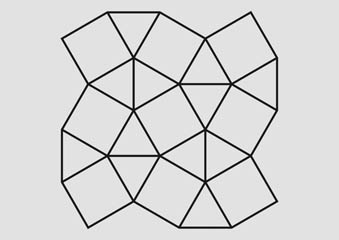
3.2. Tiling 33434. There are two Archimedean patterns in which triangles and squares are combined. In Figure 20 we see the pattern 33434 with the elevation, which is then transformed to a weaving structure in Figure 21.
Figure 20: Tiling pattern 33434.
Figure 21: Model of the elevation of the pattern 33434.