3. Folding Deltahedra (intermezzo)
3.1. Strip Plan of the Octahedron. To make an octahedron we can make a plan of eight connected triangles. We can see this as a part of triangular pattern. One way of doing this is the strip of triangles shown in Figure 8.




Figure 8: Plan of an octahedron.
Now we can extend the strip by adding pairs of triangles. The next member of this family of shapes we can create in this way is the pentagonal dipyramid. And with long strips we can create cylindrical shapes like the tetrahelix. In general most of the 3d constructions which are built with triangular faces can be "unrolled" as a strip of triangles. In Figure 9 you can see the "strip plan" of the icosahedron. There is close relationship between this "strip plan" and the Hamilton path on the dodecahedron, the dual of the icosahedron. Another nice example is the strip plan of the Kepler Star shown in Figure 10. So the group of shapes that can be formed with equilateral triangles is not only big but there are also interesting connections between the 3d shapes and the 2d plans. Reason enough for Escher to continue his research with the patterns based on the triangular grid.

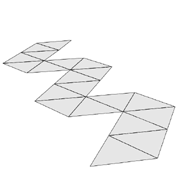
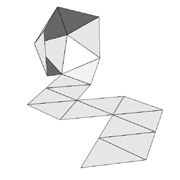

Figure 9: Icosahedron

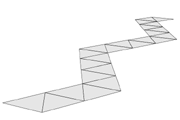
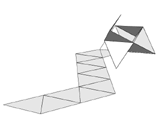
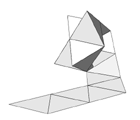
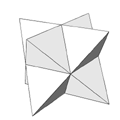
Figure 10: Kepler Star
3.2. Display B. Setting up display B in the way Escher made display A will result in the picture shown in Figure 11. Steps 1, 2 and 3 can be found in Escher's notebook. In 1950 Escher made the drawing shown in Figure 12, which can be seen as the possible fifth step for display B. It was used in one of his designs for banknotes.


Figure 11: Display B
Figure 12: Fifth pattern for Display B